The elements by Euclid 03/13/16
Would you believe it if I told you that one of the most important books ever made was in fact a Geometry textbook? How about if I told you that the same textbook had a shelf life of nearly two and a half thousand years and was only replaced very recently? And that this same textbook is also one of the foundations for the entirety of modern western thought? Well, all of the postulations are in fact complete truth. The elements is a book containing 13 volumes of treatises (all addressing different facets of mathematics). The elements begin with a simple set of postulates or innate ideas. Postulate 1: A straight line segment can be drawn between any two points. Postulate 2: Any straight line segment can be extended into an infinitely straight line. Postulate 3: Given a line segment, a circle can be drawn with that line segment as a radius.Postulate 4: All right angles are congruent. Postulate 5: If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough. This postulate is equivalent to what is known as the parallel postulate. (if it sounds strange, it’s because it has been proven to be only true in a flat space, violating this postulate gives rise to non-euclidean geometry). The elements has been a vast influence on all of western thought. The Dutch-Jewish Philosopher Spinoza created an entire system of ethics using a euclidean style of organization. Abraham Lincoln even studied the elements to assist him in his pursuit of understanding a rigorous proof for law
Month: March 2016
Transformers
Transformers 03/12/16
One of the most pertinent devices in the field of electrical engineering are transformers. The function of a transformer is very simple, it changes the potential difference from one value of wiring to another. The mechanism works a follows; The will be two wirings of coil, one on each each side of the transformer. The wire on the left will be hooked up to an alternating current which in turn will cause a magnetic field to be produced. As a by-product of Maxwell’s equations, there will be an voltage difference induced on the second coil. The voltage potential depends on the number of loops that the wire makes. If the wire has more loops then more voltage will be produced and it will be called a step up transformer. If there is less wiring there will be less voltage and it will be called a step down transformer. The equation for a transformer is VsVp=NsNp, with Vsbeing the secondary voltage Vpbeing the primary NsBeing the number of loops in the secondary and Np being the number of loops in the primary. As one can observe, The voltage ratio is directly proportional to the Loop ratio. Power also is assumed to be conserved for Mathematical purposes, so we can derive that V1I1=V1I1by using the fact that P1=P2and that P=IV.
Planetary gears
Planetary gears 03/11/16
One of the most interesting inventions ever created by the human species is are planetary gears. A problem come across by many Engineers is as follows: How can we make a smaller gear turn a larger gear while being encapsulated in it? The solution is to use a planetary gear mechanism. The trick is to use a central (smaller) gear called the sun gear to turn a multitude of other gears called “Planet gears” in the opposite direction which in turn which turn the circumferenced gear (called the “Planet gear” ) which in turn will turn. This is used frequenly in autombiles.
Modelling a pendulum using differential equations
Modelling a pendulum using differential equations 03/10/16
A most interesting intellectual exercises for anyone with a mathematical mind is to model the swing of a pendulum using differential equations. We know that the two forces that act upon a pendulum are the damping force Fdamping=-cx’and the restoring force Frestoring=-kx. When we combine this with Newton’s second law, we get mx”=-cx’-kxwhich can be rearranged to make the following second order differential equation mx”+cx’+kx=0. We can then use any solution method to solve for this differential equation
Degrees of freedom
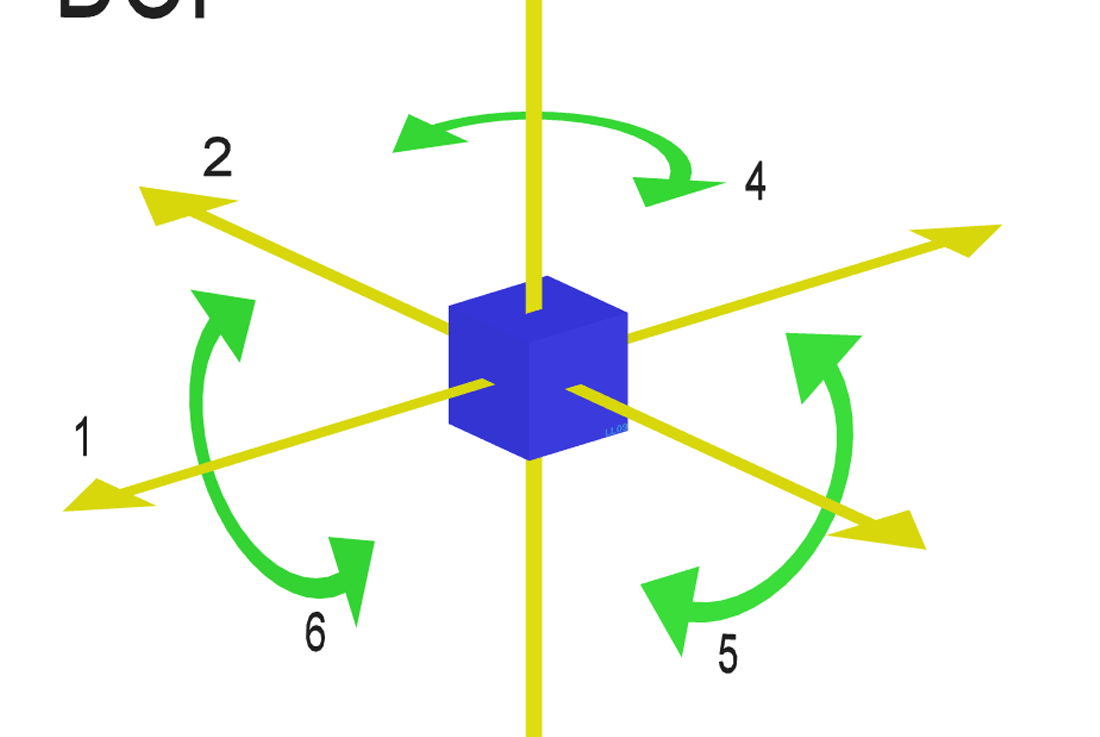
Degrees of freedom 03/09/16
In geometry and mechanics, degrees of freedom relate to the freedom of movement for an object. All objects can have up to three degrees of translational freedom (meaning they can move along the x, y, and zaxises) and three degrees of rotational freedom (the ability to rotate around the x, y, and zaxises ), therefore an object can have a maximum of six degrees of freedom. The number of degrees of freedom that an object has is contingent on it’s constraints. For example, if an object can only move on and rotate around the z axis then it has only two degrees of freedom.
Secondary Differential Equations
Secondary Differential Equations 03/08/16
During one’s course of study of mathematics, a most peculiar set of problems will arise. These problems involve not only a variable and it’s derivative of the derivative of it’s derivative! Mathematicians have labelled the problems secondary differential equations. SDQs are often written in the form ad2ydx2+bdydx+cy=0, with a,b, and c being constants. The solution for such differential equations is as follows, one supposes that the solution for yis y=erx, with r being a constant. We then substitution this postulation into the equation and factor the result. Depending on how the constants work out into the quadratic formula, if b2-4ac>0, then the solution will be y= C1er1x+C2*er2x, since the quadratic will have two distinct roots, with C1and C2being different constants as well as r1and r2. If b2-4ac=0, then the solution will be y= C1erx+C2*x*erx, with only one rsince the quadratic will only have one root. If b2-4ac<0then the solution will be y=C1*ex*cos(x)+C2*ex*sin(x)because it’s an irrational root, with and being constants.
Inductor
Inductor 03/07/16
Inductors are some of the most fundamental components of the modern day circuit. An inductor usually consists of conducting wire wrapped into a coil, and since a current will run through this wire, a magnetic field will be produced. As a result of Maxwell’s equations, the energy stored in the magnetic field will try to oppose any change in current and a voltage will be created in the inductor. The strength of an inductor is measured by it’s inductance. Inductance is defined as L=i, with Lbeing the inductance , being magnetic flux and ibeing the current. The voltage across an inductor can be symbolically derived by faraday’s law of inductance v=ddtwhich by using substitution leads to v(t) =L*didt. Inductors are widely used to tune out certain frequencies
Kirchoff’s laws
Kirchoff’s laws 03/06/16
One of the most pertinent, practical, and sublime tools for understanding circuit theory in electronics is Kirchoff’s laws. Kirchoff’s first law states that the quantity of current going through a junction is conserved going out a junction, or I=0. For a more mechanical analogy, visualize water going through a pipe. In an ideal case all of the water going through one of the pipes will either be distributed to the other two or it will collide with another one to go down the third. Kirchoff’s laws work the same way. Kirchoff’s second law states that the change in voltage across a loop always amounts to zero. One can derive this analytically using the fact that the voltage drop is the same across two parallel lines in a circuit, so consequently their voltage must equal each other and their voltage drop must equal to zero.
Magnetic fields
Magnetic fields 03/05/16
The study of magnetic fields are one of the most pertinent applications to the study of physics. Magnetic fields emanate out of the “North pole” of a magnet and emanate towards the south pole of a magnet (so technically the naming of the poles of the Earth are switched around). As a consequence of Maxwell’s equations, moving charges emit electric fields, so there is always magnetism around currents. The magnetic field only has an effect on moving charged particles that are not parallel in direction to it, since the equation for magnetic force is F=qv x B, With q being the charge v being the charge velocity and B being the magnetic field.